Confluence of Lagrange's Theorem and Elliptic Curves

A Cybersecurity Symbiosis

Synthesizing diverse mathematical concepts is crucial to fortifying digital defenses in the modern world of cybersecurity. Two such concepts, Lagrange's Theorem from group theory and Elliptic Curve Cryptography (ECC), are individually significant in their applications.

This article explores the synergistic potential of combining Lagrange's Theorem with Elliptic Curve Cryptography, elucidating how this union can lead to innovative and more robust cybersecurity solutions. 

Lagrange's Theorem

Lagrange interpolation is a mathematical method to approximate a function using a set of known data points. It is named after Joseph-Louis Lagrange, an Italian-French mathematician, and it is a fundamental technique in numerical analysis and polynomial interpolation.

One mathematical concept that finds application in encryption is Lagrange's Theorem, a result of group theory, and this “intriguing” concept can be used in cybersecurity applications, particularly encryption techniques. From secure key distribution to secret sharing schemes and ECC, the theorem enhances the security of various encryption processes.

Cybersecurity professionals can develop more robust encryption methods by incorporating mathematical principles like Lagrange's Theorem, contributing to a safer digital world. As technology advances, the integration of mathematical concepts into cybersecurity will continue to evolve, making it essential for professionals in both fields to collaborate and innovate for a secure digital future. Unfortunately, in many cases, cybersecurity professionals tend to forget the application of strongest security algorithms, as if this concept was not properly covered in their professional studies.

Lagrange's Theorem is a cornerstone in group theory, a mathematical discipline that studies the algebraic structures called groups. A group is a set equipped with an operation that satisfies specific properties. Lagrange's Theorem states that for any finite group, a subgroup's order divides the parent group's order. In simpler terms, if G is a finite group and H is a subgroup of G, then the order of H divides the order of G. 

The basic idea of Lagrange interpolation is to construct a polynomial that passes through a given set of data points. Given a set of n+1 data points (x0,y0), (x1,y1),…,(xn,yn), where each xi​ is a distinct value, and each yi​ is the corresponding function value at xi​, the Lagrange interpolation polynomial P(x) of degree n is defined as: 

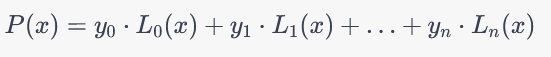
Here, Li​(x) are the Lagrange basis polynomials, which are defined as 

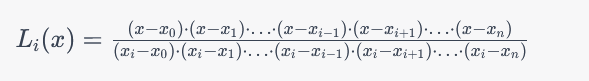
Each Li(x) is designed such that it equals 1 at xi ​and 0 at all other xj ​values. Therefore, when you compute the sum P(x), each term yi multiplied by Li​(x) contributes only to the corresponding data point xi​, resulting in a polynomial that passes through all the given data points. 

Lagrange interpolation has various applications in mathematics, physics, engineering, and computer science. It is commonly used for data approximation, curve fitting, and creating continuous functions from discrete data points. However, it is essential to note that while Lagrange interpolation provides an accurate polynomial representation of the data, it may not always be the most suitable method due to issues like Runge's phenomenon. Sometimes, other interpolation methods or techniques like splines might be preferred. 

Runge's phenomenon refers to the oscillatory behavior observed in polynomial interpolation when using equidistant interpolation points, particularly at the edges of the interval. It is known that when the degree of the interpolating polynomial grows, the polynomial may exhibit significant oscillations near the interval boundaries instead of achieving smoother approximations. This phenomenon is prominent when using equally spaced data points and high-degree polynomials, leading to undesirable results.

Runge's phenomenon underscores the limitations of using high-degree polynomials for interpolation, as it can lead to inaccurate and counterintuitive results, especially in regions where data points are sparse. To mitigate Runge's phenomenon, techniques like Chebyshev interpolation nodes or splines are employed to create more stable and accurate interpolations. Understanding Runge's phenomenon is crucial when selecting appropriate interpolation methods to ensure an accurate representation of data without introducing unintended oscillations.

Chebyshev interpolation is a method that minimizes Runge's phenomenon by selecting interpolation points based on the roots of Chebyshev polynomials. These points are distributed non-uniformly, concentrating near the interval's edges. This approach reduces oscillations in high-degree polynomial interpolations, enhancing accuracy and stability compared to equidistant interpolation points.

Application of Lagrange's Theorem in Cybersecurity 

• Cryptographic Key Distribution: In modern encryption techniques like the Diffie-Hellman key exchange, Lagrange's Theorem plays a role in secure key distribution. Parties involved in the key exchange generate their own private keys and derive a shared secret key through a series of mathematical operations. The Theorem ensures that the operations performed within the subgroup have a limited range, enhancing security by preventing certain types of attacks that exploit the properties of group operations. 

• Secret Sharing Schemes: Secret sharing schemes involve dividing a secret into multiple parts distributed among participants, where a predefined number of participants must collaborate to reconstruct the secret. Lagrange's Theorem can be applied to “guarantee” that only a specific number of participants, as determined by the order of the subgroup, can successfully reconstruct the secret. This mechanism adds a layer of security, making it computationally infeasible for fewer participants to reconstruct the secret. 

• Password Security: In password-based encryption schemes, Lagrange's Theorem can be used to enhance password storage security. By dividing the password space into subgroups, an attacker's ability to brute-force passwords is limited to a subset of possibilities. This approach strengthens the password hashing process and raises the computational cost for attackers attempting to crack passwords. One of the reasons the industry began considering that passwords are useless, is just the lack of application of mathematical theorems like Lagrange. 

Challenges and Considerations: While Lagrange's theorem offers valuable applications in cybersecurity, it is essential to note that its effectiveness depends on the proper implementation and integration within others encryption algorithms. Incorrect usage could lead to vulnerabilities and compromised security. 

There are multiple ways to generate innumerable Lagrange's Theorem diagrams, but is typically represented using set notation or a Venn diagram to illustrate the relationship between a group and its subgroups. 

Set Notation: Let G be a finite group and H be a subgroup of G. Lagrange's Theorem states that the order (number of elements) of H divides the order of G, mathematically expressed as:  

∣G∣=∣H∣ multiplied by [G divided by H] 

Here, [G divided by H] represents the index of subgroup H in-group G, which is the number of distinct cosets of H in G. 

Venn Diagram: A Venn diagram can illustrate the relationship between G and H. Imagine two circles: one representing the group G and another, smaller circle fully contained within G, representing the subgroup H. The area of H within G visually shows the concept that the order of H divides the order of G. 

It is important to note that visualizations of the Lagrange's Theorem help convey the idea behind the theorem itself as it is a mathematical statement about the sizes of sets and subgroups within a group.

Elliptic Curve Cryptography (ECC)

Among the various encryption techniques, Elliptic Curve Cryptography (ECC) stands out as a powerful and efficient method that leverages the mathematical properties of elliptic curves. ECC is a modern encryption technique based on the known characteristics of the elliptic curves over finite fields. Lagrange's Theorem is used in ECC to ensure that certain points on the elliptic curve fall within a subgroup of the curve, thereby enhancing the security of key generation and encryption processes. This helps resist attacks that rely on exploiting mathematical properties of the elliptic curve.

ECC is a public-key cryptosystem that capitalizes on the mathematical individualities of the elliptic curves completed on finite fields. The security of ECC hinges on the complexity of the Elliptic Curve Discrete Logarithm Problem (ECDLP), making it resilient against attacks from classical and quantum computers. ECC finds applications in key exchange, digital signatures, and other cryptographic protocols.

ECC is a branch of public key cryptography that revolves around the algebraic properties of elliptic curves defined over finite fields. These curves exhibit intriguing mathematical properties, containing the effort of the Elliptic Curve Discrete Logarithm Problem (ECDLP), which forms the basis for ECC's security. The ECDLP essentially involves finding the exponent that, when applied to a point on the curve, results in another given point. This problem is considered computationally infeasible to solve efficiently, even with powerful computing resources. 

Applications of Elliptic Curve Cryptography in Cybersecurity Encryption 

• Secure Key Exchange: One of the primary applications of ECC lies in secure key exchange protocols. The Diffie-Hellman key exchange and its elliptic curve variant (ECDH) allow parties to derive a shared secret key without transmitting it over the network. The security of these protocols stems from the difficulty of solving the ECDLP, which prevents eavesdroppers from deducing the shared key from the exchanged public keys. ECC's efficiency in generating smaller keys compared to traditional methods makes it ideal for resource-constrained environments like mobile devices. 

• Digital Signatures: Digital signatures are crucial for authenticating the validity and reliability of arithmetical documents or messages. ECC-based digital signature algorithms, such as ECDSA (Elliptic Curve Digital Signature Algorithm), provide a secure means of generating and verifying signatures. The compactness of ECC keys and signatures results in faster signing and verification processes, making it suitable for applications where performance is essential. 

• Public Key Infrastructure (PKI): ECC's compact key sizes are valuable in PKI systems, where storage and transmission efficiency are critical. ECC certificates and keys require less storage space, reducing the overhead associated with certificate management. This is especially beneficial in Internet of Things (IoT) scenarios, where devices may have limited memory and processing capabilities. 

• Post-Quantum Cryptography: As quantum computing advances, traditional cryptographic algorithms face the threat of being broken by quantum algorithms. ECC has emerged as a candidate for post-quantum cryptography due to its resistance against quantum attacks. This makes ECC an appealing choice for organizations seeking to ensure long-term security as quantum computers become more powerful. 

Quantum attacks are cybersecurity threats that exploit the advanced computational capabilities of quantum computers to break traditional cryptographic schemes, potentially compromising the security of sensitive data and communication. 

• Homomorphic Encryption: Homomorphic encryption allows computations to be performed on encrypted data without decryption, maintaining data privacy throughout the computation. ECC-based homomorphic encryption schemes offer a secure way to perform operations on sensitive data, making it valuable in scenarios where data privacy is paramount, such as medical research or collaborative data analysis. 

Despite its strengths, ECC is not immune to challenges. The potential for implementation errors, curve selection vulnerabilities, and side-channel attacks necessitates careful implementation and constant scrutiny. Additionally, the adoption of ECC in existing systems may require transitional efforts, as well-established systems often rely on traditional cryptography.  

Challenges and Considerations: 

• Complexity of Implementation: Integrating Lagrange's Theorem and ECC requires careful design and implementation. Mathematical precision and cryptographic expertise are essential to ensure the security and effectiveness of the combined techniques. 

• Performance Considerations: The computational overhead of Lagrange interpolation and ECC operations must be considered, especially in resource-constrained environments. Balancing security with performance is crucial for real-world applicability. 

• Cryptanalysis and Attacks: While ECC offers strong security against classical and quantum attacks, combining techniques could create new vulnerabilities. Rigorous analysis and peer review are necessary to identify and address potential weaknesses.

Lagrange's Theorem and Elliptic Curves: A Cybersecurity Symbiosis

• Secure Key Distribution: Combining Lagrange's Theorem with ECC in key exchange protocols enhances security by implementing threshold cryptography. Authorized parties generate private keys, and using Lagrange interpolation, they distribute shares of the key to designated participants. These shares are points on an elliptic curve, and the original key is recovered only when a threshold number of shares are combined. This method strengthens security against single-point vulnerabilities and cryptographic attacks, as attackers must compromise multiple shares to obtain the key. 

• Secret Sharing Schemes with ECC: Secret sharing schemes are bolstered by integrating ECC and Lagrange's Theorem. Authorized parties create shares of a secret using ECC points, and Lagrange interpolation ensures that only the intended threshold of participants can reconstruct the secret. The combination of ECC's security and Lagrange's divisibility property enables the creation of tamper-resistant secret-sharing mechanisms. 

• Multi-Party Computation (MPC): ECC-based protocols can be enhanced with Lagrange's Theorem in multi-party computation scenarios. Parties compute operations on encrypted data shares, and Lagrange's Theorem assures that the computations occur within the valid subgroup. This combination augments the privacy of computations by preventing malicious or unauthorized participants from manipulating the results. 

• Enhanced Digital Signatures: ECC's digital signature algorithms can be integrated with Lagrange's Theorem to create distributed digital signatures. Parties collaborate to generate partial signatures, and Lagrange's interpolation validates the final signature. This approach prevents a single point of compromise from affecting the entire signature, increasing security and trustworthiness in digital communication. 

To have a visual representation of the basic Elliptic Curve diagram, please note the graphic below:

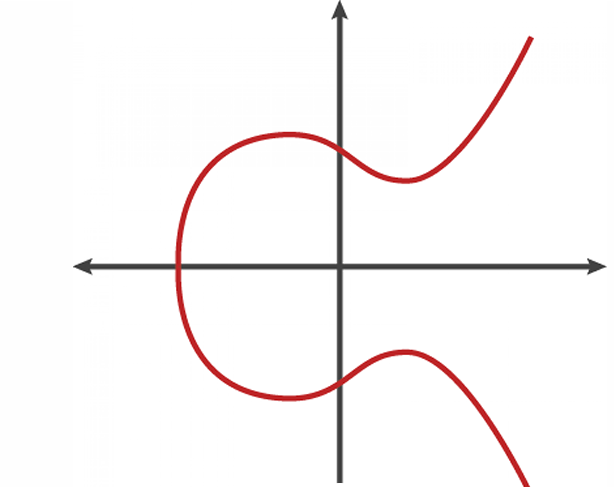
Image Source: GlobalSign Blog “ECC 101: What is ECC and why would I want to use it?” Elliptic Curve Cryptography.   

An ECC diagram represents the graphical depiction of an elliptic curve equation. The equation defining an elliptic curve is of the form: 

y2 = x3 (power of 3) + ax + b   

In a typical diagram: 

• The x-axis represents the values of the variable x. 
• The y-axis represents the values of the variable y. 
• Each point on the graph corresponds to a pair of x and y values that fulfil the requirements of the curve equation. 

An elliptic curve has distinct characteristics: 

• It is symmetric about the x-axis. 
• It may have one or more "inflection points" where the curve changes concavity. 
• It is continuous and smooth. 

The curve's shape depends on the values of the coefficients a and b in the equation. For cryptographic applications, the curve is often defined over a finite field, which introduces some additional properties.

Conclusion

The union of Lagrange's Theorem and Elliptic Curve Cryptography introduces innovative possibilities in cybersecurity. By leveraging the mathematical elegance of Lagrange's divisibility property and the computational complexity of ECDLP, practitioners can design advanced encryption protocols, key management strategies, and secure distributed systems. The combined approach enhances data protection, confidentiality, and integrity across various applications, from secure key distribution to multi-party computation and digital signatures. The harmonious integration of these mathematical concepts paves the way for resilient and future-proof cryptographic solutions that safeguard our digital world.

ECC has established itself as a fundamental pillar of modern cybersecurity encryption. Its ability to provide strong security with relatively small key sizes, efficient operations, and resistance against quantum threats makes it a versatile choice for various applications. From secure key exchange to digital signatures and beyond, ECC's mathematical elegance empowers cybersecurity professionals to design encryption solutions prioritizing confidentiality, integrity, and authenticity in the digital age. The adoption of ECC is poised to play an increasingly pivotal role in shaping the secure digital future.

References

Aalsalem, Mohammed, N Saad, Shohrab Hossain, Mohammed Atiquzzaman, and Muhammad  

Khan. 2016. “A New Random Walk for Replica Detection in WSNs.” PLoS One 11 (7): e0158072.

Blake, I. F., Seroussi, G., & Smart, N. P. (1999). Elliptic Curves in Cryptography. Cambridge University Press.

Dummit, D. S., & Foote, R. M. (2004). Abstract algebra (3rd ed.). Wiley.

Elliptic Curve Cryptography. https://www.globalsign.com/en/blog/elliptic-curve-cryptography

Fraleigh, J. B. (2018). A first course in abstract algebra. Pearson.

Gallian, J. A. (2017). Contemporary abstract algebra (9th ed.). Cengage Learning.

Hardy, G. H., & Wright, E. M. (2008). An introduction to the theory of numbers. Oxford University Press. 

Koblitz, N. (1994). A Course in Number Theory and Cryptography. Springer-Verlag. 

Lang, S. (2002). Algebra (3rd ed.). Springer.

Silverman, J. H., & Tate, J. (1992). Rational Points on Elliptic Curves. Springer-Verlag.

Washington, L. C. (2003). Elliptic Curves: Number Theory and Cryptography. Chapman & Hall/CRC.